「2023衡中同卷押题卷文综答案 」衡中同卷押题卷理综一

「2023衡中同卷押题卷文综答案 」衡中同卷押题卷理综一，目前我们已经整理了「2023衡中同卷押题卷文综答案 」衡中同卷押题卷理综一的各科答案和试卷，更多衡中同卷请关注本网站。

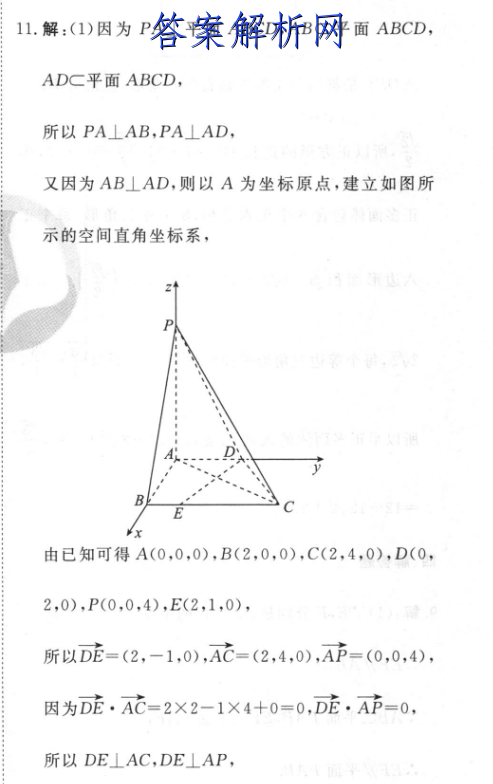
11.解：(1)因为PA⊥平面ABCD,ABC平面ABCD,ADC平面ABCD,所以PA⊥AB,PA⊥AD,又因为AB⊥AD,则以A为坐标原点，建立如图所示的空间直角坐标系，由已知可得A(0,0,0),B(2,0,0),C(2,4,0),D(0,2,0),P(0,0,4),E(2,1,0),所以DE=(2,-1,0),AC=(2,4,0),AP=(0,0,4),因为D2·AC=2×2-1×4+0=0,D苑.AP=0,所以DE⊥AC,DE⊥AP,又AP∩AC=A,APC平面PAC,ACC平面PAC,所以DE⊥平面PAC.(10分)(2)由(1)可知DE⊥平面PAC,DE=(2,-1,0)可则cos(D克，n》=DE.nIDE1·|n作为平面PAC的法向量，(12分)2×(-2)+(-1)×2+0255设平面PCD的一个法向量为n=(x,y,z),w√22+(-1)z×√(-2)2+22+1因为PD=(0,2,-4),PC=(2,4,-4).又由图示知二面角A一PC一D为锐角，n·Pb=0所以二面角A一PC-D的正弦值为5.(20分)所以n·Pt=0▣▣2y-4z=0即反馈意见有奖2x+4y-4z=0不妨设x=1,得n=(一2,2,1).(16分)

四、解答题9.解：(1)E,F分别是AC,BC的中点，EF∥AB,'ABC平面PAB,EF￠平面PAB,.EF∥平面PAB.又平面PEF∩平面PAB=I,EFC平面PEF,.EF∥l.(8分)60(2),AC,BC,PC两两垂直，AC∩BC=C,AC,BCC平面ABC,.PC⊥平面ABC,即PC是四棱锥P一ABFE的高.(10分)》,S△ABc=8,AC=BC,AC⊥BC,.'.AC=BC=4.,E,F分别是AC,BC的中点，VP-ABFE=4,∴号×是×合ACX BCX PC=-4,即PC=2.14分)∴.PA=42+2=2√5，PB=√42+22=2√5，AB=√42+4=4√2，÷△PAB的面积为号×4E×√25)2-（号）=4√6.“三棱维P-ABC的表面积S=2×合×4×2+8+4w6=16+4√6.(20分)