「2023衡中同卷答案1调理综 」衡中同卷分科综合答案

「2023衡中同卷答案1调理综 」衡中同卷分科综合答案，目前我们已经整理了「2023衡中同卷答案1调理综 」衡中同卷分科综合答案的各科答案和试卷，更多衡中同卷请关注本网站。

19.(12分)如图，在三棱锥P-ABC中，AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点，记平面AEF与平面ABC的交线为直线l.(1)证明：直线1⊥平面PAC;(2)若直线L上存在一点Q(与B都在直线AC的同侧)，且直线PQ与直线EF所成的角为牙，求平面PBQ与平面AEF所成锐二面角的余弦值.(1)证明：因为E,F分别是PC,PB的中点，所以BC∥EF.又EFC平面AEF,BC中平面AEF,所以BC∥平面AEF,又BCC平面ABC,平面AEF∩平面ABC=L,所以BC∥L.又BC⊥AC,平面PAC∩平面ABC=AC,平面PAC⊥平面ABC,所以BC⊥平面PAC,所以I⊥平面PAC.(2)解：以C为坐标原点，CA的方向为x轴正方向，CB的方向为y轴正方向，过C垂直于平面ABC的直线为z轴，建立如图所示的空间直角坐标系，E则A20,0,B0,40P1,0),E(合0，）F(分2，号）A正-(0，)，=020，设Q2,y,0),则P0=(1,y,-√3).2√4+y√4+y又Q与B都在直线AC的同侧，所以y=2,即Q(2,2,0).所以PQ=(1,2,-√3)，BQ=(2,-2,0).设平面PBQ的一个法向量为n=(xo,yo,之o),则P西n=0即+2.32=0取=1，可得m=(1,1,BQ·n=0,2xo-2yo=0,√3).313设平面AEF的一个法向量为m=(x,y,之)，则m=-2x+=0取z=3,2EF·m=2y=0,得m=(1,0,√3).所以|cos(m,n)|=1+3125√5×252√5所以平面PBQ与平面AEF所成锐二面角的余弦值为5

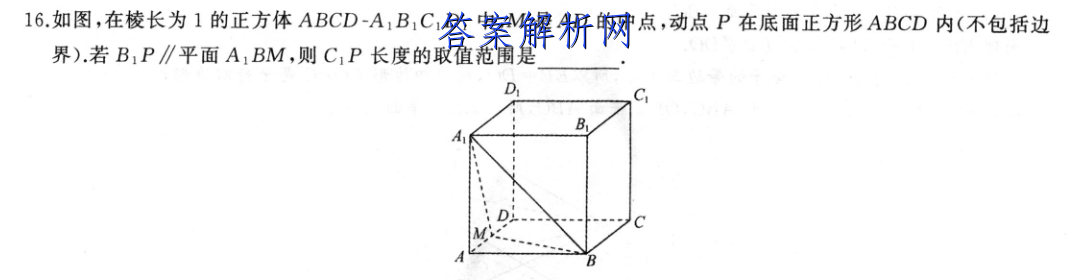
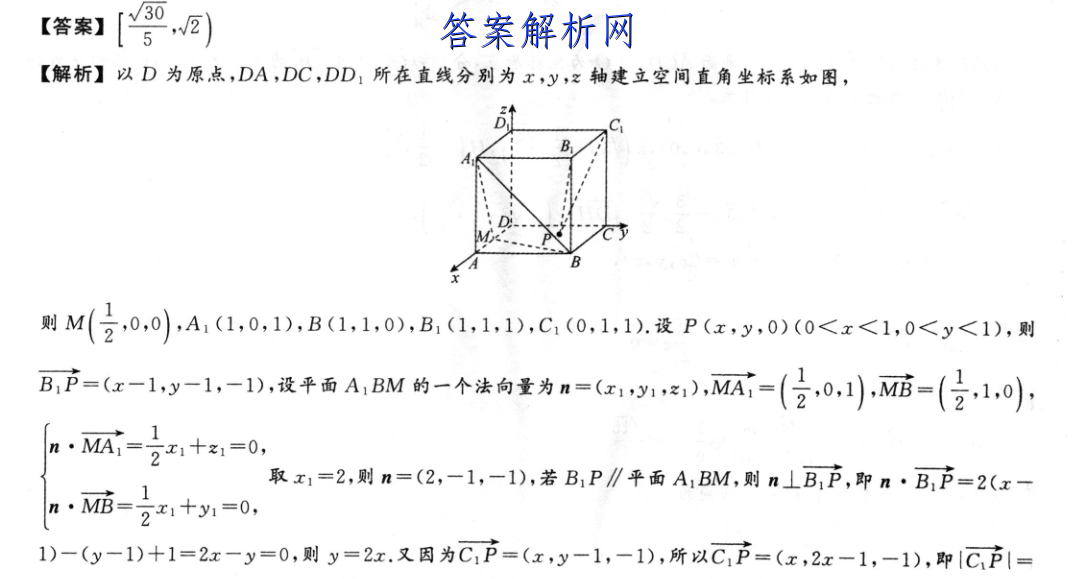
16.如图，在棱长为1的正方体ABCD-A,B1C1D1中，M是AD的中点，动点P在底面正方形ABCD内（不包括边界).若B1P∥平面A1BM,则C1P长度的取值范围是DBAD【答案】【解析】以D为原点，DA,DC,DD1所在直线分别为x,y,之轴建立空间直角坐标系如图，则M(20,0A(1,0,1),B(1,1,0),B,(1,11D,C,0,1,1D.设P(x,0)(0