「2023衡中同卷吧文综五 答案」衡中同卷高三六调文综

「2023衡中同卷吧文综五 答案」衡中同卷高三六调文综，目前我们已经整理了「2023衡中同卷吧文综五 答案」衡中同卷高三六调文综的各科答案和试卷，更多衡中同卷请关注本网站。

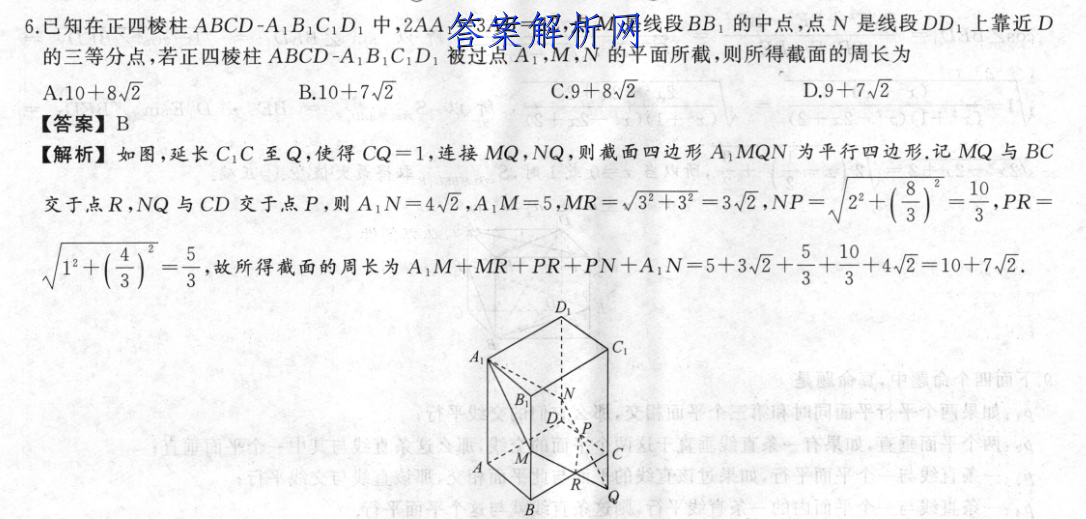
6.已知在正四棱柱ABCD-A1B1C1D1中，2AA1=3AB=12,点M是线段BB,的中点，点N是线段DD1上靠近D的三等分点，若正四棱柱ABCD-A1B1C1D1被过点A1,M,N的平面所截，则所得截面的周长为A.10+8√2B.10+7√2C.9+8√2D.9+7√2【答案】B【解析】如图，延长C1C至Q,使得CQ=1,连接MQ,NQ,则截面四边形A1MQN为平行四边形.记MQ与BC文于点R,NQ与CD交于点P,则A,N=4E.AM=5,MR=+3=3E,NP=√2+()=号，PR=P+()-号，放所得我面的周长为A,M+NMR+PR+PN+A,N=5+3E+号+智+42=10+7E.命夏，中命个面B文平个麻同面平平个西果

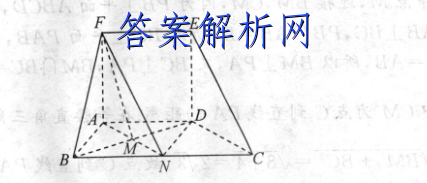
22.(12分)如图，在多面体ABCDEF中，平面ADEF⊥平面ABCD,四边形ADEF为正方形，四边形ABCD为梯形，且AD∥BC,∠BAD=90,AB=AD=2BC.(1)求证：AD∥平面BCEF;(2)求证：BD⊥平面CDE;BM(3)在线段BD上是否存在点M,使得CE儿平面AMF?若存在，求出DM的值：若不存在，请说明理由.(1)证明：因为四边形ADEF为正方形，所以AD∥EF,因为EFC平面BCEF,AD吐平面BCEF,所以AD∥平面BCEF.(2)证明：因为四边形ADEF为正方形，所以DE⊥AD因为平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,所以DE⊥平面ABCD.因为BDC平面ABCD,所以DE⊥BD.如图，取BC中点N,连接DN.由BN∥AD,BN=AD,∠BAD=90°，可得四边形ABND为正方形.所以DN=AB,所以DN=2BC.所以BD⊥CD.西0A8O因为CD∩DE=D,所以BD⊥平面CDE.FBM(3)解：存在，当M为BD的中点时，CE∥平面AMF,此时DM=1.证明如下：如图，连接AN交BD于点M,由于四边形ABND为正方形，因此M是BD的中点，同时也是AN的中点因为NC=AD,NC∥AD,又四边形ADEF为正方形，日9，OO8A面平所以NC=FE,NC∥FE,连接NF,所以四边形NCEF为平行四边形.所以CE∥NF.又因为NFC平面AMF,CE中平面AMF,BM所以CE∥平面AMF,此时M1.FEBN