「衡中同卷2023年信息栏 答案」2023届衡中同卷信息卷 全国I卷 语文(一)1答案

「衡中同卷2023年信息栏 答案」2023届衡中同卷信息卷 全国I卷 语文(一)1答案，目前我们已经整理了「衡中同卷2023年信息栏 答案」2023届衡中同卷信息卷 全国I卷 语文(一)1答案的各科答案和试卷，更多衡中同卷请关注本网站。

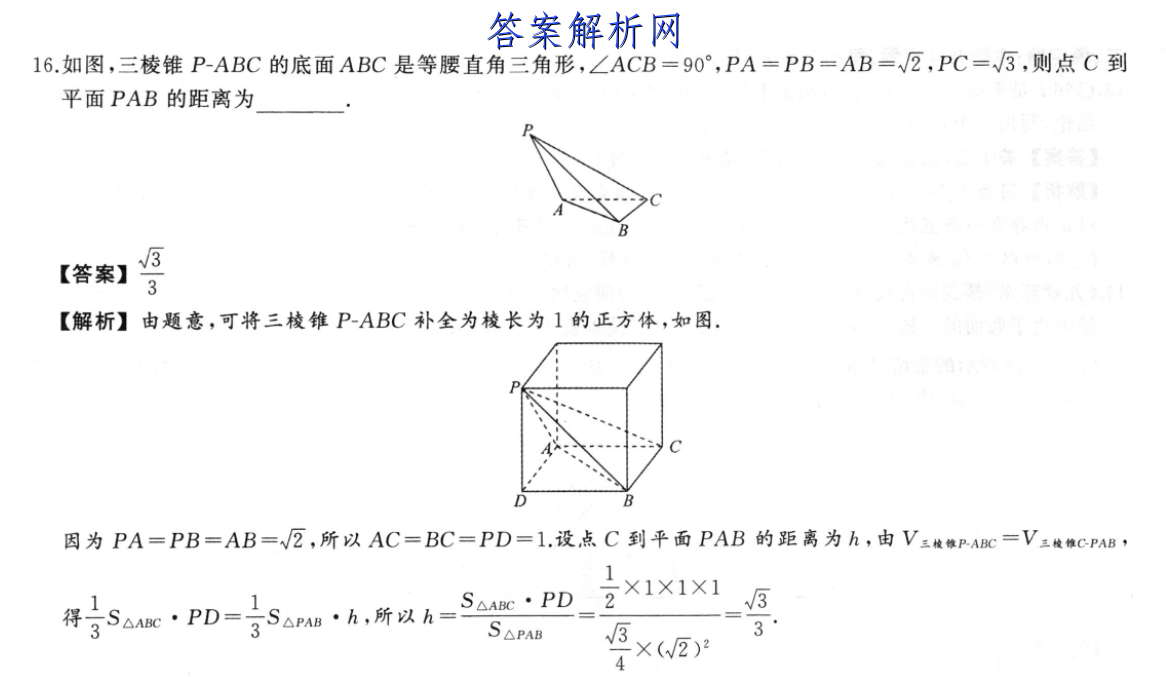
16.如图，三棱锥P-ABC的底面ABC是等腰直角三角形，∠ACB=90°，PA=PB=AB=√2，PC=√3，则点C到平面PAB的距离为【答案)【解析】由题意，可将三棱锥P-ABC补全为棱长为1的正方体，如图.CB因为PA=PB=AB=√2，所以AC=BC=PD=1.设点C到平面PAB的距离为h,由V三枚锥PABC=V三枚幢CPAB,1得号SaAe·PD=专SaPs·h,所以h=△ABC·PD1X1x13S△PAB33X(√2)24

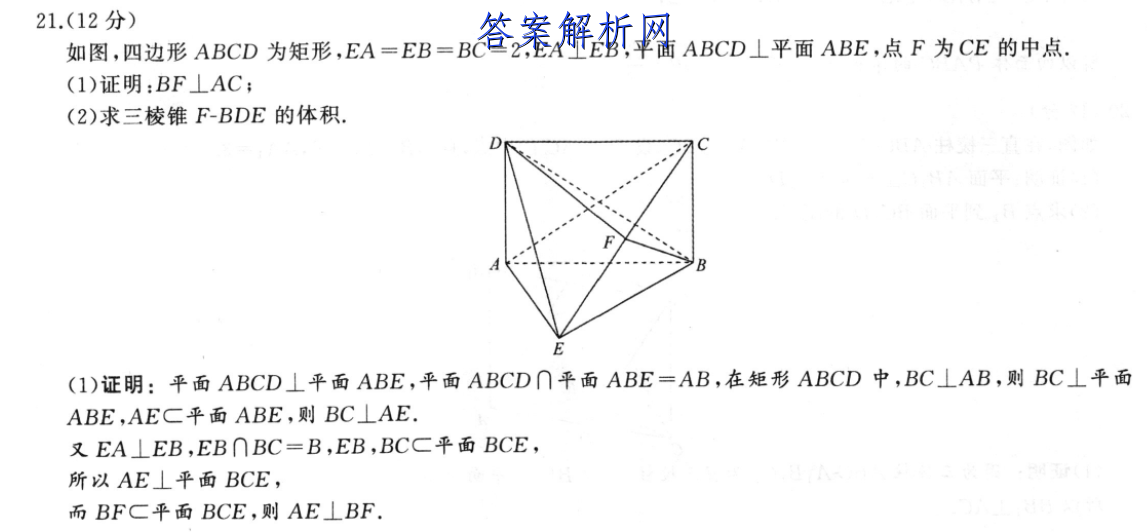
21.(12分)如图，四边形ABCD为矩形，EA=EB=BC=2,EA⊥EB,平面ABCD⊥平面ABE,点F为CE的中点，(1)证明：BF⊥AC;(2)求三棱锥F-BDE的体积.DB(1)证明：平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,在矩形ABCD中，BC⊥AB,则BC⊥平面ABE,AEC平面ABE,则BC⊥AE.又EA⊥EB,EB∩BC=B,EB,BCC平面BCE,所以AE⊥平面BCE,而BFC平面BCE,则AE⊥BF.又EB=BC,F为CE中点，所以BF⊥EC,又AE∩CE=E,AE,CEC平面ACE,从而得BF⊥平面ACE,又ACC平面ACE,所以BF⊥AC.(2)解：因为DA∥BC,DA丈平面BCE,BCC平面BCE,所以DA∥平面BCE,则点D到平面BCE的距离等于点A到平面BCE的距离.m=×BE×BC=×2x2=1,1由(1)知点A到平面BCE的距离为EA=2,S△BEF=211V三技维FBDE=V三楼#D-BEr=3·EA·S△Er=3X2X1=号所以三棱锥F-BDE的体积为2